Виктор Толстых

M-КРИВЫЕ и МЕТОД ХАРНАКА

Часть первая

      Простейшие алгебраические кривые на проективной плоскости - это прямая и эллипс. Начиная с третьей степени, вещественные алгебраические кривые могут иметь несколько несвязных компонент. К примеру, если представить прямую уравнением , а эллипс уравнением , то уравнение
       ,
где k-малый параметр, очевидно, описывает несвязную кривую третьей степени, состоящую из замкнутой компоненты-овала и незамкнутой кривой.

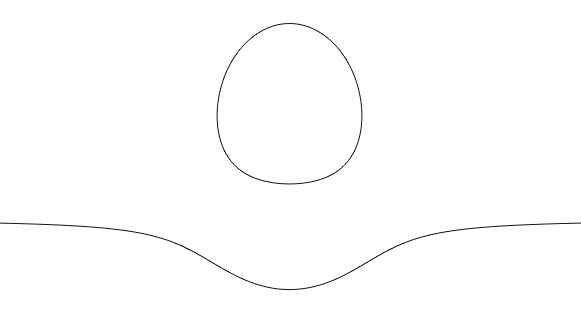
Рис.1.М-кривая степени 3

      Кривые с максимально возможным числом несвязных компонент называются
M-кривыми.  Кривые первого и второго порядка - это прямая и эллипс. Причём на проективной плоскости эллипсом считаются и парабола и гипербола. Т.е. эти
М-кривые однокомпонентны. Кривая третьей степени, как мы видим, может иметь уже две несоприкасающиеся компоненты. Сколько их вообще может быть и как они располагаются друг относительно друга для кривых до степени 6 включительно, составляет содержание первой части 16-й проблемы Гильберта.

      Для построения M-кривой четвёртой степени можно, к примеру, перемножить два пересекающихся эллипса и добавить к произведению малый параметр

. 

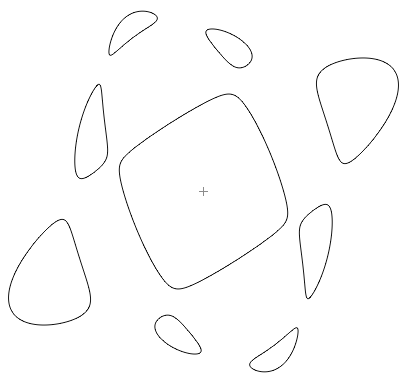
Рис.2. М-кривая степени 4

      Таким образом, мы получили 4 овала и больше их быть не может. Если допустить наличие пятой компоненты, то выберем на ней точку, а также по точке внутри каждого овала и проведём через эти пять точек единственную кривую второго порядка (т.е. эллипс в проективной плоскости). Она пересчёт нашу кривую четвёртого порядка Q минимум в 9 точках, хотя хорошо известно, что кривые 4-й и второй степени пересекаются по 4*2=8 точкам.

      Для построения M-кривой пятой степени используем взаимно пересекающиеся два эллипса и прямую

Рис.3. М-кривая степени 5

      Такая кривая имеет всего 7 компонент, из них 6 замкнутых(чётных) и одну незамкнутую(нечётную).

Часть вторая

      Начиная с шестой степени, подобная определённость заканчивается. Согласно оценке Харнака, алгебраическая кривая шестой степени может иметь до 11 компонент. И, насколько мне помнится, эта оценка получена по способу последовательного построения методом Харнака, когда к ранее построенной кривой меньшей степени добавляются новые компоненты. К примеру, кривую шестой степени S можно получить из кривой четвёртой степени Q по формуле

.

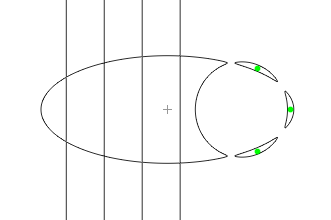
Рис.4. М-кривая степени 4 и вариация четырьмя линиями

      Малый параметр варьирует большую компоненту кривой Q, оставляя точки пересечения с 4-мя вертикальными прямыми , , и на месте. Логично предположить, что умножение на эллипс породит кривую шестой степени с 8-ю самопересечениями при . При точки пересечения исчезают, разрешаясь вот таким образом

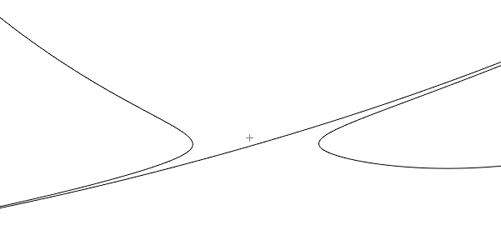
Рис.5. Пример размыкания пересечения

и получается дополнительно 7 овалов. Плюс ещё один новый овал охватывает старый овал в правой части кривой

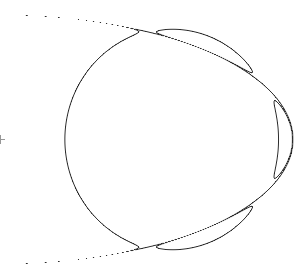
Рис.6. Правая часть кривой 6-й степени

      Таким образом, в сумме получается 3+7+1=11 компонент. (Аналогично  можно построить кривую шестой степени S из пятой P, варьируя её пятью вертикальными прямыми и умножая на ещё одну горизонтальную

 .

      Результат будет похожим - к 6+1=7 компонентам добавится ещё 5 и одна исчезнет).

      В теории метода или, скажем, в идеале должна получиться кривая примерно такого вида:

Рис.7. Гипотетическая М-кривая с 11 овалами

      Если эту кривую разомкнуть правильно по красным точкам, то мы получим 8 овалов плюс три старых овала справа, один из которых находится внутри другого большого овала. 

      На самом деле эта кривая идеальна и искусственно синтезирована из двух в программе Photoshop. В реальности, как только мы начинаем варьировать кривую Q четвёркой вертикальных прямых с коэффициентом , 3 компоненты Q справа тут же бесследно исчезают (при значении коэффициента <1.0. Варьирование не может быть сколь угодно малым, поскольку из-за вариации коэффициентом k, при получении Q из и , левый компонент кривой Q уже не является эллипсом и имеет определённый зазор с эллипсом . Пока мы ликвидируем этот микроскопический зазор (при >1000.0), все три компоненты справа исчезают. При этом, что совсем обескураживает, появляется дополнительная чётная компонента, причём совсем не там, где её ожидали. Это свидетельствует в пользу того, что никаких компонент справа не должно было остаться.
Вот так:

Рис.8. Кривая с 9 овалами

      Или даже вот так:

Рис.9. Кривая с 9 овалами. Внешний овал представлен как часть гиперболы

      Как ни старайся, а больше 9 компонент не получить!
     

      Я пока не знаю в чём тут загвоздка. Но кое-что нехорошее уже можно сказать в адрес самой харнаковской процедуры построения M-кривых. Она - недостаточно строгая.
     

Часть третья

      А теперь давайте вернёмся назад к синтезированной кривой 6 и докажем, что она не может существовать.

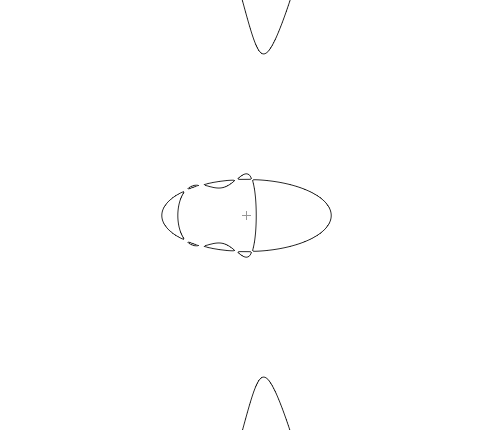
      Зафиксируем три из четырёх пар точек пересечения слева набором из трёх вертикальных линий в этих узлах

.

      При и кривая будет выглядеть вот так

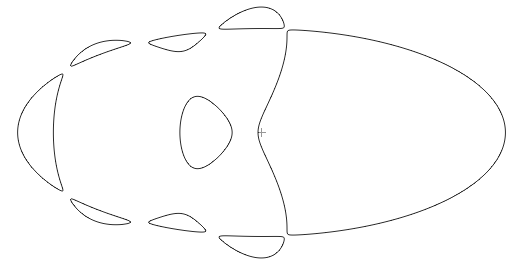
Рис.10. Вариация с фиксацией 6-ти точек

      Эта кривая имеет 6 точек самопересечения, расположенных строго по эллипсу, причём участки линий между узлами не лежат на эллипсе, поскольку подверглись вариации. Через эти 6 точек проходит как единственный эллипс, так и множество кубических кривых, в том числе распадающихся на этот эллипс и некую прямую. Но, вместе с тем, они могут быть и не распадающимися, поскольку пересекаются по разумному числу точек 2*3=6.

      Сделаем теперь аналогичную вариацию, но уже для всех 4-х пар точек самопересечения . Дорисуем также недостающие компоненты справа и расставим 9 узлов для 3-кривой - восемь красных и  один зелёный

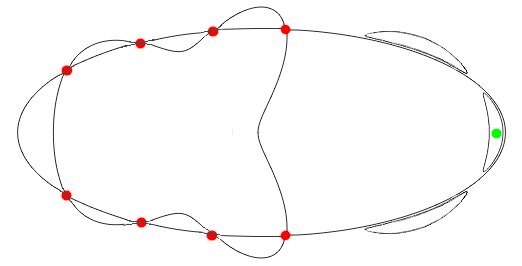
Рис.11. Гипотетическая модель перед размыканием

      Проведём через красные и зелёные 9 точек единственную кубическую кривую. Она пересекает кривую шестой степени в 8 красных точках строго по эллипсу, причём между этими точками при больше совпадений нет. Она  также проходит через зелёный узел внутри вложенного овала справа. 
      Поскольку кубическая кривая пересекает 8 точек эллипса, т.е. больше положенного 2*3=6, то она, очевидно, по этому эллипсу совпадает с самим эллипсом. Т.е. является распадающейся на эллипс и прямую. Таким образом, остаётся, что через зелёную точку пройдёт другая компонента этой распадающейся кубической кривой, т.е. - прямая.
Прямая пересечёт два вложенных овала по 4 точкам - не меньше. Следовательно, имеем при подсчёте 8 двойных пересечений в красных узлах и 4 одинарных пересечения около зелёной точки. Т.е. 8*2 +4*1=20. Это на 2 больше максимально допустимого значения 6*3=18. Т.е. такой конструкции быть не может.
 

Резюме:

      Похоже, что сама харнаковская процедура последовательного построения M-кривых нуждается в основательной ревизии. Таким образом ставятся под сомнение теоретически построенные Харнаком, Гильбертом, Гудковым и пр. многочисленные М-кривые степени от 6 и выше. Так же ставится под сомнение утверждение о том, что 16-я проблема Гильберта решена. Может быть и решена, но с перебором - М-кривых меньше чем даёт этот метод.

  
      А что дальше? Остаётся выяснить существуют ли вообще кривые 6 степени с 10 и 11 компонентами, раз харнаковская процедура под вопросом. При этом, для значения 9 пока мы видим два очевидных варианта расположения: все 9 компонент снаружи или 8 компонент внутри одной:

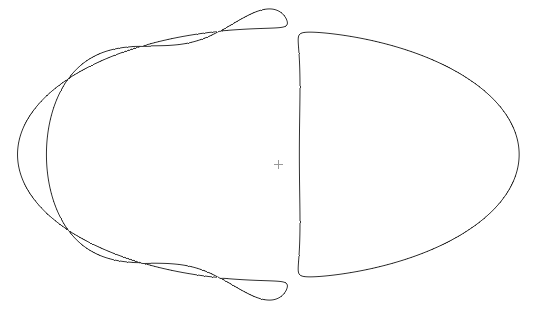
Рис.12. Кривая с 9 не вложенными овалами

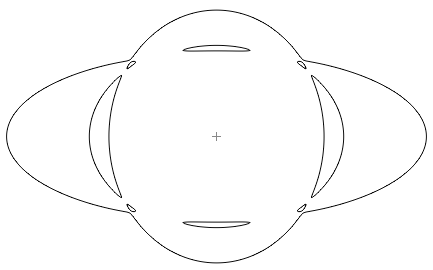
Рис.13. Кривая с 8 овалами, вложенными в один

Есть ли ещё варианты?
Мне почему-то кажется, что это всё.
 

СПб, 28 янв. 2006